cubist_rules() defines a model that derives simple feature rules from a tree
ensemble and creates regression models within each rule. This function can fit
regression models.
There are different ways to fit this model, and the method of estimation is chosen by setting the model engine. The engine-specific pages for this model are listed below.
Cubist¹²
More information on how parsnip is used for modeling is at https://www.tidymodels.org/.
Usage
cubist_rules(
mode = "regression",
committees = NULL,
neighbors = NULL,
max_rules = NULL,
engine = "Cubist"
)Arguments
- mode
A single character string for the type of model. The only possible value for this model is "regression".
- committees
A non-negative integer (no greater than 100) for the number of members of the ensemble.
- neighbors
An integer between zero and nine for the number of training set instances that are used to adjust the model-based prediction.
- max_rules
The largest number of rules.
- engine
A single character string specifying what computational engine to use for fitting.
Details
Cubist is a rule-based ensemble regression model. A basic model tree
(Quinlan, 1992) is created that has a separate linear regression model
corresponding for each terminal node. The paths along the model tree are
flattened into rules and these rules are simplified and pruned. The parameter
min_n is the primary method for controlling the size of each tree while
max_rules controls the number of rules.
Cubist ensembles are created using committees, which are similar to
boosting. After the first model in the committee is created, the second
model uses a modified version of the outcome data based on whether the
previous model under- or over-predicted the outcome. For iteration m, the
new outcome y* is computed using
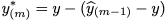
If a sample is under-predicted on the previous iteration, the outcome is adjusted so that the next time it is more likely to be over-predicted to compensate. This adjustment continues for each ensemble iteration. See Kuhn and Johnson (2013) for details.
After the model is created, there is also an option for a post-hoc adjustment that uses the training set (Quinlan, 1993). When a new sample is predicted by the model, it can be modified by its nearest neighbors in the original training set. For K neighbors, the model-based predicted value is adjusted by the neighbor using:
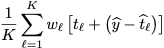
where t is the training set prediction and w is a weight that is inverse
to the distance to the neighbor.
This function only defines what type of model is being fit. Once an engine
is specified, the method to fit the model is also defined. See
set_engine() for more on setting the engine, including how to set engine
arguments.
The model is not trained or fit until the fit() function is used
with the data.
Each of the arguments in this function other than mode and engine are
captured as quosures. To pass values
programmatically, use the injection operator like so:
value <- 1
cubist_rules(argument = !!value)References
https://www.tidymodels.org, Tidy Modeling with R, searchable table of parsnip models
Quinlan R (1992). "Learning with Continuous Classes." Proceedings of the 5th Australian Joint Conference On Artificial Intelligence, pp. 343-348.
Quinlan R (1993)."Combining Instance-Based and Model-Based Learning." Proceedings of the Tenth International Conference on Machine Learning, pp. 236-243.
Kuhn M and Johnson K (2013). Applied Predictive Modeling. Springer.
